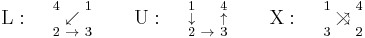Conway's LUX method for magic squares
Conway's LUX method for magic squares is an algorithm by John Horton Conway for creating magic squares of order 4n+2, where n is a natural number.
Method
Start by creating a (2n+1)-by-(2n+1) square array consisting of
- n+1 rows of Ls,
- 1 row of Us, and
- n-1 rows of Xs,
and then exchange the U in the middle with the L above it.
Each letter represents a 2x2 block of numbers in the finished square.
Now replace each letter by four consecutive numbers, starting with 1, 2, 3, 4 in the centre square of the top row, and moving from block to block in the manner of the Siamese method: move up and right, wrapping around the edges, and move down whenever you are obstructed. Fill each 2x2 block according to the order prescribed by the letter:
Example
Let n = 2, so that the array is 5x5 and the final square is 10x10.
-
L L L L L L L L L L L L U L L U U L U U X X X X X
Start with the L in the middle of the top row, move to the 4th X in the bottom row, then to the U at the end of the 4th row, then the L at the beginning of the 3rd row, etc.
-
68 65 96 93 4 1 32 29 60 57 66 67 94 95 2 3 30 31 58 59 92 89 20 17 28 25 56 53 64 61 90 91 18 19 26 27 54 55 62 63 16 13 24 21 49 52 80 77 88 85 14 15 22 23 50 51 78 79 86 87 37 40 45 48 76 73 81 84 9 12 38 39 46 47 74 75 82 83 10 11 41 44 69 72 97 100 5 8 33 36 43 42 71 70 99 98 7 6 35 34